Байгальд бүхий л зүйлс харилцан шүтэлцээтэй, нэгдмэл байдлаар оршдог. Тиймээс байгалийн ухаанд ч нэг нэгнээс нь салангид биш, нэгдмэл байдлаар суралцуулж, суурь мэдлэг олгоход анхаарах хэрэгтэй.Олон улсын томхон сургуулиуд энэ талаар өөрсдийн бодлоготой, оюутнуудын хичээл сонголтоор дамжуулж түүнийгээ хэрэгжүүлдэг. Дэлхийд дээгүүр эрэмбэлэгддэг Токиогийн Их Сургуульд байгалийн ухаан эсвэл инженерчлэлийн чиглэлээр суралцах бүх оюутан байгалийн ухааны суурь болгож дараах хичээлүүдийг тус бүр хоёр улирал заавал судалдаг.
- Математик анализ
- Шугаман алгебр
- Физик
- Хими
- Туршилт
Дээрээс нь нэмээд бүгд мэдээлэл зүй хичээлийг нэг улирал, мөн олонх оюутнууд термодинак, хэлбэлзэл ба долгион хичээлүүдийг нэг нэг улирал сонгон судалдаг. Математикч, физикч, химич эсвэл геологич болох уу, компьютрийн инженер, электроникийн инженер эсвэл хэрэглээний математикч болох уу ялгаагүй. Мөн хичээлийн агуулга ч адилхан[1]. Өөрөөр хэлбэл химийн инженер болох оюутан физикч болох оюутантай яг адилхан физикийн хичээл үзнэ гэсэн үг. Мэдээж гадаад хэл болон хүмүүнлэг, нийгмийн ухааны хичээлүүдийг ч тодорхой хэмжээнд үзэх ёстой.
Тэгвэл манай улсад байгалийн ухааны суурь мэдлэг олгох боловсрол ямар байдалтай олгогдож байна вэ? МУИС-ийн хувьд олон жилийн туршид бүх сургууль, тэнхимүүд нь тусдаа явснаас байгалийн ухааны суурь хичээл гэх юм огт байсангүй. Жишээлбэл Математик Компьютерийн Сургуулийн оюутан механикаас эхлээд оптик, квант физик зэрэг бүх физикийг 1 улиралд багтаан үздэг байсны дээр хими бол огт үздэггүй байв. Харин 2014 оноос эхлэн хэрэгжсэн бүтцийн өөрчлөлт болон хөтөлбөрийн шинэчлэлээр МУИС-ийн ерөнхий суурь хичээлд зориулан 45 багц цаг гаргаж өгснөөр суурь хичээлүүд нэгтгэгдэж, оюутнууд харьцангуй тэгш ерөнхий суурь боловсрол эзэмших боломж, эхлэл нь тавигдсан гэж хэлж болно. Харамсалтай нь Шинжлэх Ухааны Сургуулийн Байгалийн Ухааны Сургууль (ШУС, БУС) болон Хэрэглээний Шинжлэх Ухаан, Инженерчлэлийн Сургуулийн (ХШУИС) суурь хичээлүүд үндсэндээ огтлолцолгүй, салангид хэвээрээ байна. Жишээ нь өнөөдөр математикийн тэнхимд элссэн оюутан физик, химийн хичээл огт үзэхгүй төгсөх бүрэн боломжтой. Харамсалтай гэж хэлж байгаа шалтгаан нь орчин үеийн байгалийн шинжлэх ухаанууд хоорондоо салшгүй холбоотой, нэгийг нь салгаж сураад сайн судлаач, мэргэжилтэн болох боломжгүйд бий. Жишээ нь өндөр түвшний математикийн мэдлэггүйгээр сайн физикч, химич эсвэл мэдээлэл зүйч болох ямар ч боломжгүй юм[2]. Математик, физик, хими болон биологийн холбоог харуулсан нэгэн сонгодог жишээ нь битүү зангилааны онол юм. Энэ жишээний тухай астрофизикч M. Livio “Is God a Mathematician?” Бурхан математикч уу? номондоо нэлээн дэлгэрэнгүй өгүүлсэн байдаг.
Байгалийн ухааны уялдаа холбоо, түүхэн жишээ:
Одоогоос 150 гаруй жилийн өмнө буюу 1860-аас оны үед Английн алдарт физикч W. Thompson (бидний мэддэгээр Лорд Келвин) химийн элемент буюу атом нь этэр гэх зүйлээс бүтсэн битүү зангилаа байж болох юм гэсэн санаа дэвшүүлэв. Тухайн үед химийн элементүүдийн химийн шинж чанарыг тодорхой хэмжээгээр ойлгож байсан боловч үүний цаад учрыг тайлбарлах физикийн онол гарч ирээгүй байлаа[3]. Битүү зангилаа гэдэг нь доорх зурагуудаар илэрхийлсэн мэт хоёр үзүүрийг нь холбосон зангилаа юм.
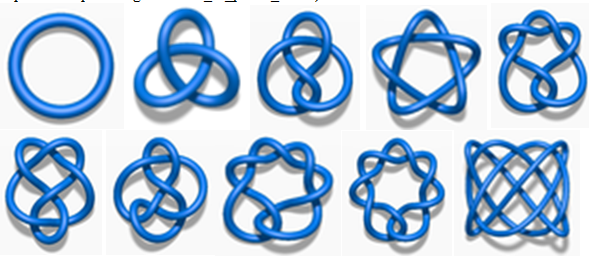
Зургийн эх сурвалж: http://en.wikipedia.org/wiki/List_of_prime_knots)
Битүү зангилааны математик онолын үндсэн асуулт нь хоёр битүү зангилааг таслахгүйгээр, тасралтгүй өөрчлөлтөөр нэгийг нь нөгөө рүү нь шилжүүлж болох уу гэдэг асуулт юм. Та жишээ болгоод дараах хоёр битүү зангилааг нэгээс нь нөгөөрүү нь шилжүүлж болох эсэхийг бодож үзээрэй. (Энэ хоёр битүү зангилааны тухай дараах хуудаснаас дэлгэрэнгүй уншиж болно: http://en.wikipedia.org/wiki/Perko_pair)
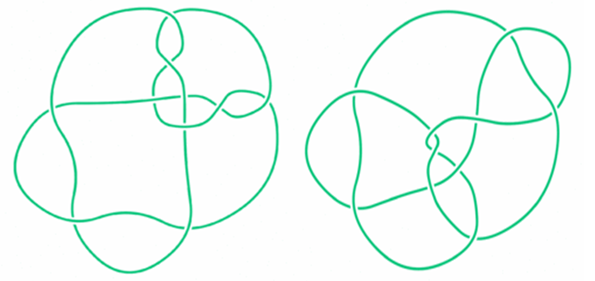
Лорд Келвин химийн элементүүд төрөл бүрийн битүү зангилаанд харгалзах бөгөөд тэднийг харгалзах зангилааг нь судлах замаар тайлбарлаж болно гэж таамаглажээ. Ингэхийн тулд тэрээр юуны өмнө битүү зангилаануудыг үелэх системтэй төстэй хэлбэрээр ангилах шаардлагатай болсон байна. Битүү зангилааг математикчид түүнээс даруй 90 жилийн өмнөөс судалж байжээ. Мэдээж Лорд Келвиний таамаглал битүү зангилааны онолын хөгжилд том түлхэлт өгсөн бөгөөд 1877 он гэхэд түүний найз Шотландын математикч физикч П. Тэйт 7 хүртэл зөрлөгтэй бүх битүү зангилаануудыг ангилжээ. Тэрээр 1885 онд 10 хүртэл зөрлөгтэй битүү зангилаануудын хүснэгтийг хэвлүүлсэн байдаг.
Харамсалтай нь XX зууны эхээр Дирак, Хайзенберг нарын квант онол гарсанаар Томсоний онол буруу болох нь батлагдан физикээс хасагдаж, битүү зангилааны онол математикийн нэгэн жижиг салбар болон үлдэж. Зангилааны онолд 1928 онд Америкийн математикч Ж. Александер зангилааг ялгах шинэ арга, мөн 1960-аад оны сүүлчээр Англи-Америк математикч Ж. Конвэй зангилааг тайлах шинэ арга нээсэн боловч өөр доривтой амжилт гаралгүй хэдэн арваныг үдэв. Харин 1984 онд Шинэ Зеланд – Америк математикч В. Жонс битүү зангилаануудыг ялгах цоо шинэ арга нээлээ. Тэрээр фон Нойман алгебр гэдэг хийсвэр математикийн онолын судалгаа хийж байгаад үндсэндээ санамсаргүйгээр тэр аргыг нээсэн байна. Жонс энэ ажилаараа математикийн хамгийн нэр хүндтэй шагналуудын нэг болох Фиелдсийн шагналыг хүртжээ.
Энд түүхийн сонин нугалаа гэхээр зүйл болсон нь фон Нойман алгебр нь Дирак, Хайзенбергийн квант онолын математик суурийг тавих оролдлогоос үүсэн гарсан явдал юм. Цаашилбал, дээр дурдсан Тэйт битүү зангилааны ангиллыг хийх явцдаа хэд хэдэн таамаглал дэвшүүлсэн нь батлагдахгүй удсан ч эхнийх нь Жонсын нээлтийн дараа Жонсын аргыг ашиглан батлагджээ. Өөрөөр хэлбэл физикийн онолын судалгаанаас урган гарсан математик таамаглал нь физикийн онолын судалгаанаас урган гарсан математик аргачлалыг ашиглан батлагдсан байх юм. Бусад таамаглалууд нь ч тун удахгүй батлагдсан.
Түүхийн нугалаа үүгээр зогсоогүй. Жонсын нээлт битүү зангилааны онолд цоо шинэ түлхэлт өгч, судалгаанууд идэвхижив. Улмаар зангилааны онол орчин үеийн физикийн хамгийн чухал онолын нэг болох нумын онолтой холбоотой болох нь тогтоогдож, битүү зангилааны онол физикт эргэн ирсэн юм. Нумын онол нь физикийн бүх хүчийг нэгдсэн нэг онолоор тайлбарлах гэсэн оролдлого юм. Одоогоор татах хүчний онол болох Айнштайны харьцангуй онолыг цөмийн хүчний онол болох квант механикийн онолтой холбож чадсан онол гараагүй байгаа агаад нумын онолыг үүнд хамгийн ойрхон онолын нэг гэж үздэг. (Харамсалтай нь Ч. Эрдэнэ гуайн “Супернэгдлийн Онол” бол математикийн ч онол биш, физикийн ч онол биш болохыг энд дурдахгүй өнгөрч чадсангүй).
Эцэст нь биологид ч гэсэн битүү зангилааны онол хэрэглэгддэг тухай товчхон өгүүлье. Deoxyribonucleic acid буюу DNA нь бүх амьд биетийн генийн мэдээллийг кодлодог молекул болохыг та мэдэх биз. DNA-г электрон дурангаар харахад доорх зураг буюу (битүү) зангилаа гардаг байх нь.
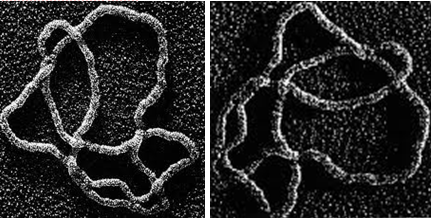
Зургийн эх сурвалж: http://kids.britannica.com/comptons/art-122745/The-shape-of-a-strand-of-DNA-photographed-with-an http://www.popmath.org.uk/exhib/pagesexhib/appl1.html
Ерөнхийдөө DNA нь маш урт ээдрээтэй зангилаа байдаг бөгөөд хуваагдах, хуулагдахын тулд энзайм гэж нэрлэгддэг тусгай молекулаар зангилаагаа тайлуулах шаардлагатай болдог, тэр нь дээр дурдсан Конвэйн зангилаа тайлах аргатай яг адилхан юм. Иймээс биологичид битүү зангилааны онол ашиглан өгөгдсөн энзаймийн үйлчлэлийн хурдыг хэмждэг байна. Ингэж битүү зангилааны онол математик, физик, хими, биологийн ухааны дунд нэг нэгнээс нь санаа аван хөгжиж, аль алиных нь хөгжилд үйлчилж ирсэн түүхтэй.
Энэ мэт байгалийн ухаан хоорондын хамтын хөгжил, харилцан шүтэлцээ, санамсаргүй эргэлтийн жишээгээр шинжлэх ухааны түүх арвин. Суурь шинжлэх ухаануудын ерөнхий суурь боловсролыг сайн олгож байж дэлхий ертөнцийн баялаг нууцаас шинжлэх ухааны түлхүүрээр нээх, анзаарах боловсон хүчин Монголд төрнө.
Тайлбар:
[1] Зөвхөн математик анализийн хичээлийг тооцоо голдуу, баталгаа голдуу гэж хоёр өөр хувилбараар заадаг бөгөөд оюутанууд дуртайгаа сонгох эрхтэй.
[2] Байгалийн шинжлэх ухаануудын уялдаа холбооны талаар бичигдсэн олон өгүүлэл, ном зохиол байдаг. Тухайлбал математикийн бусад байгалийн ухаанд гүйцэтгэх итгэмээргүй гэмээр үүргийн талаар 1960 онд хэвлэгдсэн Принстоны Их Сургуулийн профессор Нобелийн шагналт физикч E. Wigner-ийн бичсэн
- The Unreasonable Effectiveness of Mathematics in the Natural Sciences
өгүүлэл тухайн үедээ олон хүний анхаарал татаад зогсоогүй, өнөөдөр сонгодог өгүүлэлийн тоонд зүй есоор тооцогддог. Энэ өгүүлэлийн хариу болгож бичсэн эсвэл энэ өгүүлэлээс сэдэвлэж бичсэн олон өгүүлэл байдгаас хэдхэнийг дурдвал:
- Hamming (1980), The unreasonable effectiveness of mathematics
- Schoeder (1992), The unreasonable effectiveness of number theory in physics, communication and music
- Jackiw (1999), The unreasonable effectiveness of quantim field theory
- Lesk (2000), The unreasonable effectiveness of mathematics in molecular biology
- Atiyah (2002), On the unreasonable effectiveness of physics in mathematic
[3] 1869 онд Оросын химич Д. Менделеев “Элементүүдийн Үелэх Систем”-ээ хэвлүүлсэн.






математик онол биш юу юм лалар минь. супер онолыг үгүйсгэж байгаа бол няцаалт бичээд олон нийтэд цац. тоон тооцоог яаж няцаахыг чинь харая. Танай тэр Дашдорж гэж өвгөн математикч супер нэгдлийн онол гэж яриад байгаа нь шал худлаа гэсэн байсан. Нэгдүгээрт, ерөөсөө философи яриагүй математик, тэр дундаа цэвэр математик ярьж байна, математикч хүн тэр ч худлаа энэ ч худлаа гэж амаараа шаадаггүй юм. Баталгаа эсвэл няцаалт хийгээд цацаад аль. Аль 2010 онд нэгдсэн онолын ном гарсан ч одоог хүртэл баталгаа ч юмуу няцаалт ч юмуу тиймэрхүү юм 'математикч' та нараас олж үзээгүй л байгаа шүү бааснууд минь. [email protected]